Aplicación de la función
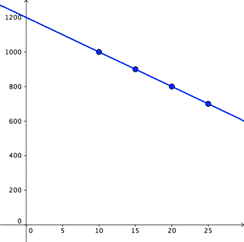
Graficar s en el eje horizontal y qen el eje vertical. Usar dos puntos cualesquiera en la línea recta de la gráfica para encontrar la pendiente de la recta que es -20. Leer la intersección en y como 1200.
Poner estos valores en la forma pendiente-intersección (y = mx + b):
q = -20s + 1200
q = -20s + 1200
q = cantidad vendida
s = precio de venta del artículo
La fórmula de la ganancia es P = Ingresos Totales – Costos de Producción
Ingresos Totales = precio • cantidad vendida
Costos de Producción = costo por artículo • cantidad vendida
Entonces P = sq – 10q
| |||
P = s(-20s + 1200) – 10(-20s + 1200)
|
Sustituir -20s + 1200 por q en la fórmula de la ganancia
| ||
P = -20s2 + 1200s + 200s – 12000
P = -20s2 + 1400s – 12000
|
Multiplicar las expresiones y combinar los términos comunes. Ahora tenemos una ecuación cuadrática.
Encontrando el vértice de la parábola, encontraremos el precio de venta que generará la ganancia máxima. El eje xrepresenta el precio de venta, por lo que el valor de la coordenada x en el vértice, representa el mejor precio.
El valor de y en el vértice nos dará la cantidad de ganancias hechas
| ||
|
| |||
El precio de venta que genera la máxima ganancia es $35
|
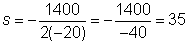
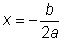

Comentarios
Publicar un comentario